height of binary tree queries

 2458. Height of Binary Tree After Subtree Removal Queries

Solved
Hard
Topics
Companies
Hint

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

  • Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

  • The queries are independent, so the tree returns to its initial state after each query.
  • The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

 

Example 1:

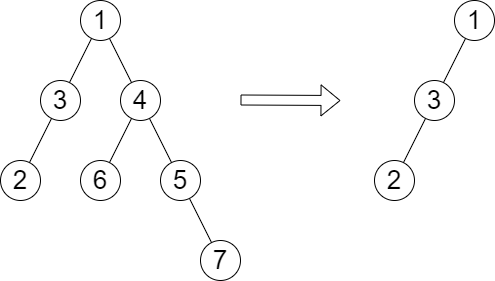
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

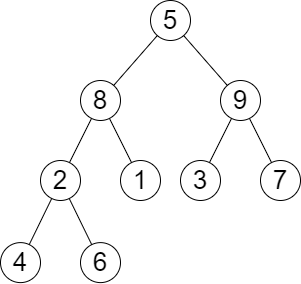
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

 

Constraints:

  • The number of nodes in the tree is n.
  • 2 <= n <= 105
  • 1 <= Node.val <= n
  • All the values in the tree are unique.
  • m == queries.length
  • 1 <= m <= min(n, 104)
  • 1 <= queries[i] <= n
  • queries[i] != root.val

  • Solution

    Overview

    The approaches outlined below have similar time and space complexities. Rather than representing significant improvements over one another, they offer different methods and perspectives for solving the problem. You can either review all of them and choose the one that appeals to you, or explore each one in detail to understand the various ways to tackle the problem.

    Approach 1: Left and Right Traversal

    Intuition

    The problem asks us to find the height of a tree (the longest path from the root) after removing a subtree rooted at nodes listed in queries.

    A brute force solution would process each query separately by removing the specified subtree and recalculating the height of the remaining tree. However, this approach is inefficient due to its high time complexity.

    To optimize, we can track the tree's height as we traverse from the root. For any node, the height after removing its subtree is simply the height of the tree before reaching that node. This allows us to avoid recalculating the height repeatedly.

    We’ll perform a preorder traversal, tracking the maximum distance from the root. However, if the maximum height is achieved in the right subtree, we may miss it when traversing the left. To address this, we perform a second traversal in reverse preorder (root, right, left).

    We maintain an array heights where heights[i] stores the tree height after removing the subtree rooted at node i. During the first traversal, we update heights with the height at each node as we explore its left and right subtrees. In the reverse traversal, we update heights if the current height is greater than the stored value.

    Finally, we iterate over queries and return the corresponding heights for each specified node.

    Algorithm

    • Initialize:
      • a static array maxHeightAfterRemoval to store the maximum height of the tree after removing each node.
      • a variable currentMaxHeight to 0, which will track the current maximum height during traversals.

    Main method treeQueries:

    • Call the traverseLeftToRight method with the root node and initial height 0.

    • Reset currentMaxHeight to 0 for the second traversal.

    • Now call the traverseRightToLeft method with the root node and initial height 0.

    • Initialize an array queryResults to store the results of the queries.

    • Iterate through the queries:

      • For each query, retrieve the corresponding maximum height from maxHeightAfterRemoval.
      • Store this height in queryResults.

    • Return the queryResults array.

    • Define a method traverseLeftToRight:

      • If the current node is null, return.
      • Store the current currentMaxHeight in maxHeightAfterRemoval for the current node's value.
      • Update currentMaxHeight to be the maximum of itself and the current height.
      • Recursively call traverseLeftToRight for the left and right child, incrementing the height.

    • Define a method traverseRightToLeft:

      • If the current node is null, return.
      • Update maxHeightAfterRemoval for the current node's value to be the maximum of its current value and currentMaxHeight.
      • Update currentMaxHeight to be the maximum of the current height and itself.
      • Recursively call traverseRightToLeft for the right and left child, incrementing the height.

        Approach 2: Single Traversal

        Intuition

        Let's optimize our solution to use just one traversal. We'll perform a preorder traversal starting from the root, similar to our previous approach. During this traversal, we’ll track a variable maxVal representing the maximum height encountered so far.

        For each node, we store its corresponding answer (the maxVal at that point) in a resultMap for quick lookups during queries. We’ll also keep track of the depth as we traverse.

        To determine the maximum height if a node is removed, we consider two values:

        1. The current maxVal on the path from the root to the node.
        2. The node’s depth plus one (to include itself) and the height of its sibling subtree.

        To calculate the height of a sibling subtree, we’ll use a memoized helper function that finds the maximum distance from a given node to its leaf nodes.

        Starting the DFS from the root, we populate resultMap with heights for each node. Once the traversal completes, we can answer queries using the information stored in resultMap.

        Algorithm

        • Initialize a map:

          • resultMap to store the maximum height of the tree after removing each node.
          • heightCache to store pre-computed heights of subtrees.

        • Call the dfs method with initial parameters: root node, depth 0, maxVal 0, resultMap, and heightCache.

        • Initialize an array result to store the final query results.

        • Iterate through the queries:

          • For each query, retrieve the corresponding maximum height from resultMap.
          • Store this height in the result array.

        • Return the result array.

        • Define the height method to calculate the height of a tree:

          • If the node is null, return -1.
          • If the height of the node is already in heightCache, return the cached value.
          • Calculate the height recursively as 1 plus the maximum of left and right subtree heights.
          • Store the calculated height in heightCache.
          • Return the calculated height.

        • Define the dfs method for the depth-first search:

          • If the current node is null, return.
          • Store the current maxVal in resultMap for the current node's value.
          • Recursively call dfs for the left child:
            • Increment the depth.
            • Update maxVal as the maximum of current maxVal and (depth + 1 + height of right subtree).
          • Recursively call dfs for the right child:
            • Increment the depth.
            • Update maxVal as the maximum of current maxVal and (depth + 1 + height of left subtree).

              Approach 3: Subtree Size

              Intuition

              In a preorder traversal of a tree, a subtree starts at its root's index and ends at the index equal to the start index plus the subtree's size. If we know the index and size of the subtree to be removed, we can remove this section from the traversal list. The maximum depth in the remaining traversal then represents the tree’s maximum height after removal.

              For example, given the indices and depths of nodes, removing a subtree will leave us with the highest depth among the remaining nodes as our answer. To understand this better, have a look at the visualization below:

              To implement this, we’ll perform a preorder traversal to:

              1. Assign an index to each node
              2. Track the depth of each node

              We then create two arrays, maxDepthsFromLeft and maxDepthsFromRight, to store the maximum depth to the left and right of each index, respectively. These arrays are filled by iterating through the nodes and updating each index with the maximum of the previous result and the current node’s depth.

              Finally, to process each query, we compute the result as the maximum of:

              1. The maximum depth from the left up to the starting index
              2. The maximum depth from the right beyond the ending index, if available.

              Algorithm

              • Initialize a map:

                • nodeIndexMap to store the index of each node value.
                • subtreeSize to store the number of nodes in the subtree for each node.

              • Initialize lists nodeDepths, maxDepthFromLeft, and maxDepthFromRight to store node depths and maximum depths from left and right.

              • Call the dfs method to populate nodeIndexMap and nodeDepths.

              • Store the total number of nodes in totalNodes.

              • Call calculateSubtreeSize method to populate the subtreeSize map.

              • Initialize maxDepthFromLeft and maxDepthFromRight with the first and last node depths respectively.

              • Iterate through the nodes to calculate maxDepthFromLeft and maxDepthFromRight:

                • Update maxDepthFromLeft with the maximum of the previous max and current depth.
                • Update maxDepthFromRight with the maximum of the previous max and current depth (in reverse order).

              • Reverse the maxDepthFromRight list.

              • Initialize an array results to store the query results.

              • Process each query. For each query node:

                • Calculate the end index as the node's index minus 1.
                • Calculate the start index as the end index plus the subtree size plus 1.
                • Initialize maxDepth with the value from maxDepthFromLeft at the end index.
                • If the start index is within bounds, update maxDepth with the maximum of current maxDepth and the value from maxDepthFromRight at the start index.
                • Store the maxDepth in the results array.

              • Return the results array.

              • Define a method dfs for the depth-first search:

                • If the current node is null, return.
                • Add the current node's value and index to nodeIndexMap.
                • Add the current depth to nodeDepths.
                • Recursively call dfs for left and right children, incrementing the depth.

              • Define a method calculateSubtreeSize :

                • If the current node is null, return 0.
                • Recursively calculate the size of left and right subtrees.
                • Calculate the total size as left size plus right size plus 1.
                • Store the total size in subtreeSize for the current node.
                • Return the total size.

                • Approach 4: Eulerian Tour

                  Intuition

                  The previous approach can be generalized using an Eulerian tour. An Eulerian tour traverses the tree such that each node is visited twice, once when first encountered, and again when leaving after exploring all its subtrees.

                  In this tour, a subtree is bounded by the first and last occurrences of its root node. To find the maximum height of the tree after removing a subtree, we can simply look at the maximum depth before the first occurrence and after the last occurrence of the subtree's root node.

                  To create the Eulerian tour, we perform a DFS over the tree, recording the first and last occurrences of each node in the firstOccurrence and lastOccurrence maps, respectively, while tracking each node's depth.

                  Like the previous approach, we calculate maxDepthLeft and maxDepthRight for each node for quick access. For each query, we can then retrieve the maximum depths at the first and last occurrences of the queried node and return the greater of the two as our answer.

                  Algorithm

                  • Initialize a list eulerTour to store the Euler tour of the tree.

                  • Initialize maps nodeHeights, firstOccurrence, and lastOccurrence to store information about each node.

                  • Call the dfs function to build the Euler tour and populate the maps.

                  • Set tourSize to the size of eulerTour.

                  • Initialize arrays maxDepthLeft and maxDepthRight of size tourSize.

                  • Set the first element of maxDepthLeft and last element of maxDepthRight to the height of the root node.

                  • Iterate from 1 to tourSize - 1:

                    • Set maxDepthLeft[i] to the maximum of the previous max height and the current node's height.

                  • Iterate backward from tourSize - 2 to 0:

                    • Set maxDepthRight[i] to the maximum of the next max height and the current node's height.

                  • Initialize an array results with the same length as queries.

                  • For each query in queries:

                    • Set queryNode to the current query value.
                    • Calculate leftMax and rightMax as the max height to the left and right of the node's first occurrence, respectively.
                    • Store the maximum of leftMax and rightMax in results.

                  • Return the results array.

                  • Define the dfs function:

                    • If the current node is null, return.
                    • Add the current node's height to nodeHeights.
                    • Set the first occurrence of the current node in firstOccurrence.
                    • Add the current node's value to eulerTour.
                    • Recursively call dfs for left and right children, incrementing the height.
                    • Set the last occurrence of the current node in lastOccurrence.
                    • Add the current node's value to eulerTour again.

  • Approach 5: Two Largest Cousins

    Intuition

    At any node, the longest path through it is the sum of its depth and the height of its subtree. For each depth, the maximum tree height at that level will be the depth plus the maximum height of any node at that depth.

    To optimize this, we organize nodes by their depths and precalculate their heights. If a query removes a node, we find the maximum height at that depth, excluding the removed node.

    To streamline further, the maximum height from a given depth can be found using two precomputed values:

    1. The maximum height at that depth, excluding the current node.
    2. The second-highest height at that depth, if the maximum height subtree is removed.

    Thus, we only need the two largest heights at each depth. We maintain two lists, firstLargestHeight and secondLargestHeight, where each index stores the two largest heights for each depth. We then use DFS to populate these lists, along with each node's depth and height. For each query, if a node’s height matches the largest height at its depth, we return the second-largest height at that level; otherwise, we return the largest height.

    Algorithm

    • Initialize a map:

      • nodeDepths to store the depth of each node.
      • subtreeHeights to store the height of the subtree rooted at each node.

    • Initialize maps firstLargestHeight and secondLargestHeight to store the first and second largest heights at each level.

    • Call the dfs function to populate these maps.

    • Initialize an array results with the same length as queries.

    • For each query in queries:

      • Set queryNode to the current query value.
      • Set nodeLevel to the depth of the query node.
      • If the height of the query node's subtree equals the first largest height at its level:
        • Set the result to the sum of node level and second largest height at that level, minus 1.

    • Otherwise:

      • Set the result to the sum of node level and first largest height at that level, minus 1.

    • Return the results array.

    • Define the dfs function:

      • If the current node is null, return 0.
      • Add the current node's depth to nodeDepths.
      • Recursively call dfs for left and right children, incrementing the level.
      • Calculate currentHeight as 1 plus the maximum of left and right subtree heights.
      • Add the current node's subtree height to subtreeHeights.
      • Set currentFirstLargest to the first largest height at the current level.
      • If currentHeight is greater than currentFirstLargest:
        • Update secondLargestHeight at the current level with currentFirstLargest.
        • Update firstLargestHeight at the current level with currentHeight.
      • Else if currentHeight is greater than the second largest height at the current level:
        • Update secondLargestHeight at the current level with currentHeight.
      • Return currentHeight.

Comments

Post a Comment

Popular posts from this blog

LeetCode 3Sum

Question Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0. Notice that the solution set must not contain duplicate triplets. Brute force We can run 3 loops to check each possible triplets, we also need to eliminate the duplicates from both sides. this method will work but will work but will give time limit exceed after time constraints. To do this in given time limit we need to sort the array first and Create a loop that fixes the left most integer. This reduces the problem to 2sum for remaining array. For each loop iteration where duplicates are skipped, we need to do a left/right iteration using while loop. my code:
Read more

Heap (min)

 Heap Heap is a data structure used to store numbers in form of binary tree i.e each node has two children. Heap is the data structure behind PriorityQueue. Insert and pop operation inside a heap is oh log(n) complexity and can be used in multiple insert and pop operation questions. It is efficient and used in fastest sorting as well as sorting only takes nlog(n) complexity at worst case. Important Functions for heap: 1.  Heapify: This function is a top down approach to set an given array into heap. The idea is to set the top priority Item at the parent node of given subtree of 3. We will compare priority of left item from parent and then from right item to that of winner of parent and left and then swap the top priority with parent item. If top priority wasn't the parent item then we call the heapify again for the right or left node with which the value was swapped. If we have a given array then we can run a loop into that array from bottom of tree to top (excluding leafs),i....
Read more

New start Day 2 (1/10/2020) codeforces 492B Vanya and Lantern

 question: (source: https://codeforces.com/problemset/problem/492/B)      Vanya And Lantern Vanya walks late at night along a straight street of length  l , lit by  n  lanterns. Consider the coordinate system with the beginning of the street corresponding to point  0 , and its end corresponding to the point  l . Then the  i -th lantern is at the point  a i . The lantern lights all points of the street that are at the distance of at most  d  from it, where  d  is some positive number, common for all lanterns. Vanya wonders: what is the minimum light radius  d  should the lanterns have to light the whole street? Input The first line contains two integers  n ,  l  ( 1 ≤  n  ≤ 1000 ,  1 ≤  l  ≤ 10 9 ) — the number of lanterns and the length of the street respectively. The next line contains  n  integers  a i  ( 0 ≤  a i  ≤  l ). Multiple lanterns can be loca...
Read more