Modify Graph Edge Weights

 You are given an undirected weighted connected graph containing n nodes labeled from 0 to n - 1, and an integer array edges where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.

Some edges have a weight of -1 (wi = -1), while others have a positive weight (wi > 0).

Your task is to modify all edges with a weight of -1 by assigning them positive integer values in the range [1, 2 * 109] so that the shortest distance between the nodes source and destination becomes equal to an integer target. If there are multiple modifications that make the shortest distance between source and destination equal to target, any of them will be considered correct.

Return an array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from source to destination equal to target, or an empty array if it's impossible.

Note: You are not allowed to modify the weights of edges with initial positive weights.

 

Example 1:

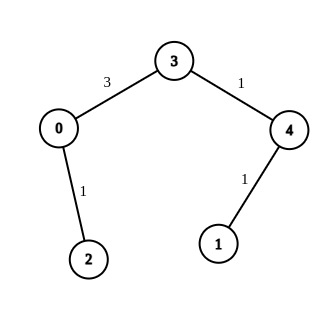
Input: n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
Output: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
Explanation: The graph above shows a possible modification to the edges, making the distance from 0 to 1 equal to 5.

Example 2:

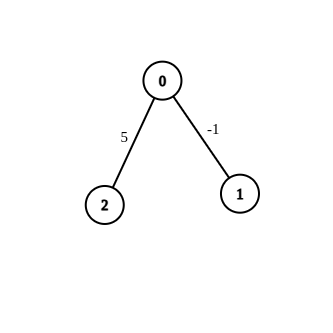
Input: n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
Output: []
Explanation: The graph above contains the initial edges. It is not possible to make the distance from 0 to 2 equal to 6 by modifying the edge with weight -1. So, an empty array is returned.

Example 3:

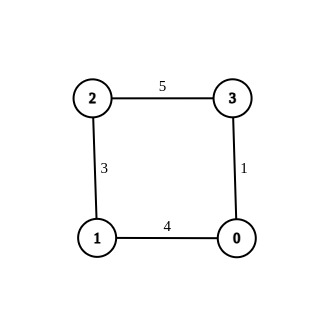
Input: n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
Output: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
Explanation: The graph above shows a modified graph having the shortest distance from 0 to 2 as 6.\

Intution:
for every edgfe that is not negative, perform dikstra and check if current distance from source to destination is less than target then we cannot modify any node to reach target, if we already at the target then modify every -1 weighted edge as max value, if current distance is > target for every edge i.e -1 change it to 1 and add to graph and run dikstra, if new distance is greater than target, move to next -1 node. if it is less than target then update last added edge value to difference of target and current distance. for remaining edges make them max weighted.
If shortest distance is greater than target even after modifying all edges then nothing can be done.

Comments

Post a Comment

Popular posts from this blog

LeetCode 3Sum

Question Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0. Notice that the solution set must not contain duplicate triplets. Brute force We can run 3 loops to check each possible triplets, we also need to eliminate the duplicates from both sides. this method will work but will work but will give time limit exceed after time constraints. To do this in given time limit we need to sort the array first and Create a loop that fixes the left most integer. This reduces the problem to 2sum for remaining array. For each loop iteration where duplicates are skipped, we need to do a left/right iteration using while loop. my code:
Read more

New start Day 2 (1/10/2020) codeforces 492B Vanya and Lantern

 question: (source: https://codeforces.com/problemset/problem/492/B)      Vanya And Lantern Vanya walks late at night along a straight street of length  l , lit by  n  lanterns. Consider the coordinate system with the beginning of the street corresponding to point  0 , and its end corresponding to the point  l . Then the  i -th lantern is at the point  a i . The lantern lights all points of the street that are at the distance of at most  d  from it, where  d  is some positive number, common for all lanterns. Vanya wonders: what is the minimum light radius  d  should the lanterns have to light the whole street? Input The first line contains two integers  n ,  l  ( 1 ≤  n  ≤ 1000 ,  1 ≤  l  ≤ 10 9 ) — the number of lanterns and the length of the street respectively. The next line contains  n  integers  a i  ( 0 ≤  a i  ≤  l ). Multiple lanterns can be loca...
Read more

Heap (min)

 Heap Heap is a data structure used to store numbers in form of binary tree i.e each node has two children. Heap is the data structure behind PriorityQueue. Insert and pop operation inside a heap is oh log(n) complexity and can be used in multiple insert and pop operation questions. It is efficient and used in fastest sorting as well as sorting only takes nlog(n) complexity at worst case. Important Functions for heap: 1.  Heapify: This function is a top down approach to set an given array into heap. The idea is to set the top priority Item at the parent node of given subtree of 3. We will compare priority of left item from parent and then from right item to that of winner of parent and left and then swap the top priority with parent item. If top priority wasn't the parent item then we call the heapify again for the right or left node with which the value was swapped. If we have a given array then we can run a loop into that array from bottom of tree to top (excluding leafs),i....
Read more