1631. Path With Minimum Effort

 You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

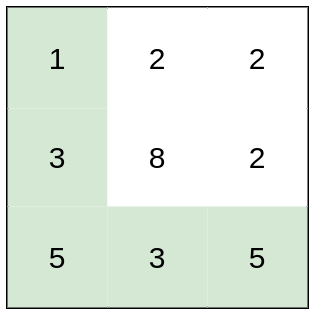
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

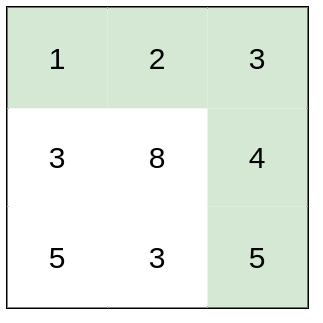
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

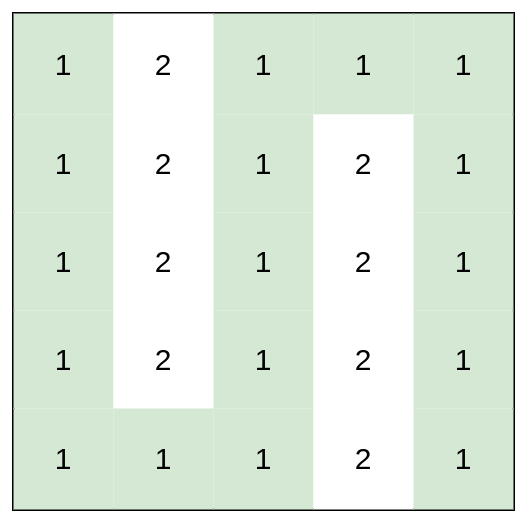
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

  • Key Concepts and Constraints

    What Makes This Problem Unique?

    1. Graph Representation:
      This problem can be mapped to a graph where each cell in the 2D matrix is a node. The edges connecting these nodes represent the "effort" required to move from one cell to another.

    2. Variants of Shortest Path Algorithms:
      The objective is similar to finding the shortest path, but with a different metric. We need to minimize the maximum absolute difference between adjacent nodes.

    3. Constraints:

      • 1≤rows, columns≤1001 \leq \text{rows, columns} \leq 100
      • 1≤heights[i][j]≤1061 \leq \text{heights}[i][j] \leq 10^6

    Strategies to Tackle the Problem

    1. Dijkstra's Algorithm:
      A classic algorithm for finding the shortest path in a weighted graph, adapted for this problem.

    2. Dijkstra's Algorithm Explained

      What is Dijkstra's Algorithm?

      Dijkstra's Algorithm is a classic graph algorithm that finds the shortest path from a source node to all other nodes in a weighted graph. In this case, the graph is represented by a 2D grid of cells, where each cell is a node and the edges between them represent the effort to move from one cell to another.

      Mechanics of Dijkstra's Algorithm in "Path With Minimum Effort"

      1. Initialize Priority Queue:

        • The algorithm starts at the top-left corner (the source). The priority queue is initialized to store the effort needed to reach each cell from the source. The effort for the source itself is zero.

      2. Distance Matrix:

        • A 2D array keeps track of the minimum effort required to reach each cell. Initially, this is set to infinity for all cells except the source.

      3. Iterate and Update Distances:

        • The algorithm pops the cell with the smallest effort from the priority queue and explores its neighbors. The effort required to reach a neighbor is updated if a smaller effort is found.

      4. Early Exit:

        • The algorithm stops when it reaches the bottom-right corner, returning the effort required to get there.

      Time and Space Complexity

      • Time Complexity: O(M×Nlog⁡(M×N))O(M \times N \log(M \times N)), where MM and NN are the dimensions of the grid. This is primarily due to the operations on the priority queue.
      • Space Complexity: O(M×N)O(M \times N), needed for the distance matrix and the priority queue.

Comments

Post a Comment

Popular posts from this blog

LeetCode 3Sum

Question Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0. Notice that the solution set must not contain duplicate triplets. Brute force We can run 3 loops to check each possible triplets, we also need to eliminate the duplicates from both sides. this method will work but will work but will give time limit exceed after time constraints. To do this in given time limit we need to sort the array first and Create a loop that fixes the left most integer. This reduces the problem to 2sum for remaining array. For each loop iteration where duplicates are skipped, we need to do a left/right iteration using while loop. my code:
Read more

New start Day 2 (1/10/2020) codeforces 492B Vanya and Lantern

 question: (source: https://codeforces.com/problemset/problem/492/B)      Vanya And Lantern Vanya walks late at night along a straight street of length  l , lit by  n  lanterns. Consider the coordinate system with the beginning of the street corresponding to point  0 , and its end corresponding to the point  l . Then the  i -th lantern is at the point  a i . The lantern lights all points of the street that are at the distance of at most  d  from it, where  d  is some positive number, common for all lanterns. Vanya wonders: what is the minimum light radius  d  should the lanterns have to light the whole street? Input The first line contains two integers  n ,  l  ( 1 ≤  n  ≤ 1000 ,  1 ≤  l  ≤ 10 9 ) — the number of lanterns and the length of the street respectively. The next line contains  n  integers  a i  ( 0 ≤  a i  ≤  l ). Multiple lanterns can be loca...
Read more

Heap (min)

 Heap Heap is a data structure used to store numbers in form of binary tree i.e each node has two children. Heap is the data structure behind PriorityQueue. Insert and pop operation inside a heap is oh log(n) complexity and can be used in multiple insert and pop operation questions. It is efficient and used in fastest sorting as well as sorting only takes nlog(n) complexity at worst case. Important Functions for heap: 1.  Heapify: This function is a top down approach to set an given array into heap. The idea is to set the top priority Item at the parent node of given subtree of 3. We will compare priority of left item from parent and then from right item to that of winner of parent and left and then swap the top priority with parent item. If top priority wasn't the parent item then we call the heapify again for the right or left node with which the value was swapped. If we have a given array then we can run a loop into that array from bottom of tree to top (excluding leafs),i....
Read more